误差范围是由于测量系统中的随机变量所致，并遵循统计规则。学习这些规则以及如何应用规则是我们估算光谱测量误差范围的步。

如何分布随机变量

群体中单个变量的值范围落在所谓的正态分布或钟形曲线范围内。 

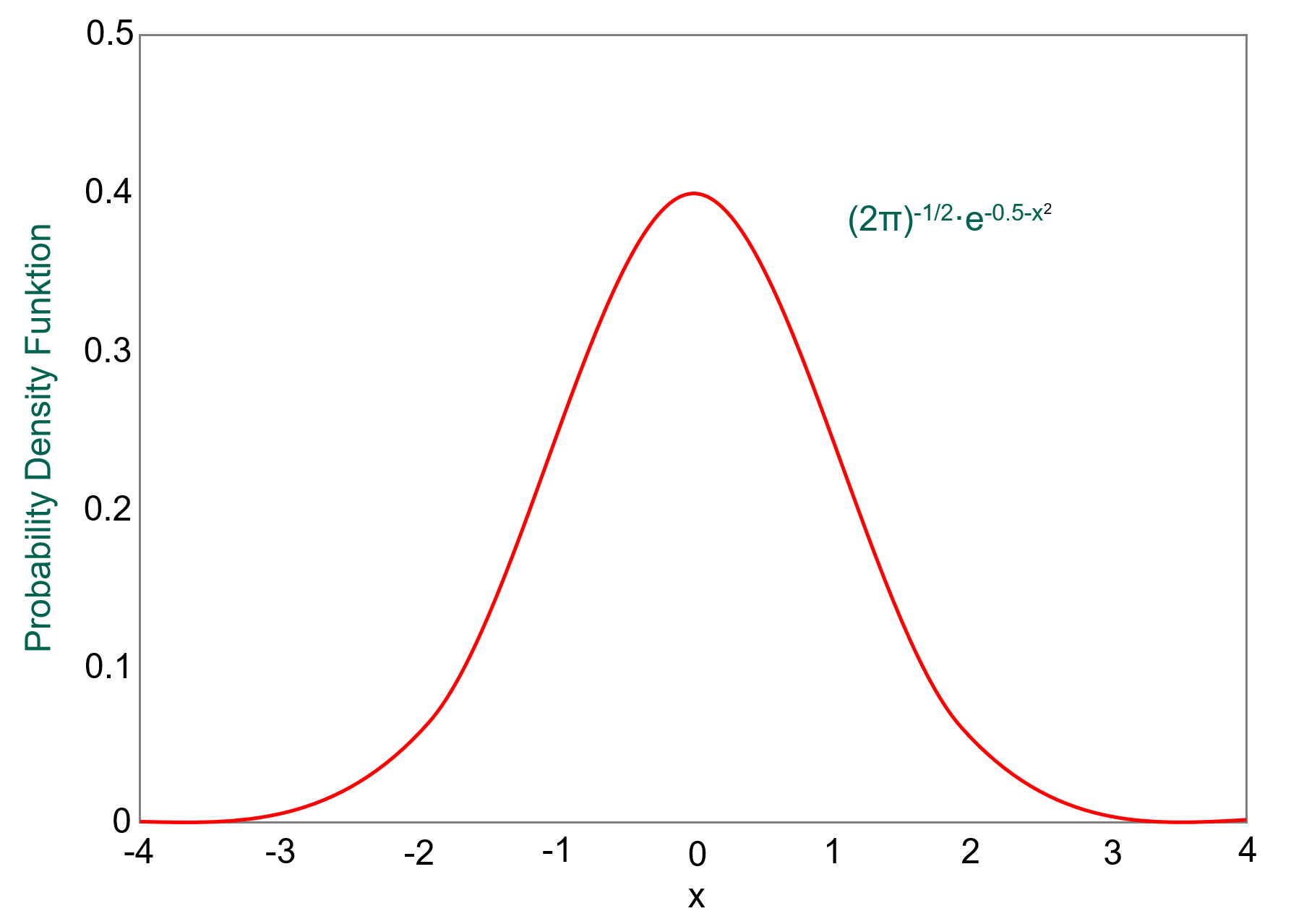
以身高为例，假设我们测量所有女性的身高，然后绘制图表，以y轴表示身高，x轴表示该身高对应的女性人数。该图表将具有上述正态分布曲线的形状，具有平均身高的大多数人位于中央部分，非常高和非常矮的女性数量则向两侧递减。

什么是标准偏差？

如果我们看一下正态分布曲线，我们可以看到形状越宽，存在的值越远离平均值。曲线越窄意味着值越接近平均值。用σ表示的标准偏差提供了一个数值，用以说明结果的分布情况。 

对于正态分布，情况始终如此：

68.25％的结果落在离平均值一个标准偏差（1σ）范围内

95.45％的结果落在离平均值两个标准偏差（2σ）的范围内

99.73％的结果落在离平均值三个标准偏差（3σ）的范围内

对于光谱测量，标准偏差值越小，正态分布曲线越窄，测量越。标准偏差（σ）可通过以下公式计算：

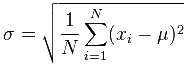
其中:

μ：群体平均值

xi：个体测量值

N：进行的测量次数

现实世界应用

在现实世界中，我们通常不会测量全部群体。相反，我们会测量一个群体样本。

在我们的光谱学领域中，我们通常不会通过测量足够大的样本量来计算全部群体的σ。相反，我们会测量一个群体样本。幸运的是，在这种情况下，我们可以使用略微修改的表达式来估算样本标准偏差。我们使用符号s来表示样本的标准偏差。

s的表达式如下：

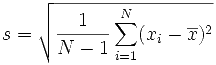
其中：

x̅： 所有测量的平均值

x i： 个体测量值

N： 进行的测量次数

我们可以使用此样本标准偏差（s）来估算光谱测量中的误差范围。如果我们想要获得准确率为95％的结果——并且记住，对于正态分布，95.45％的结果落在离平均值两个标准偏差的范围内——我们终会得到：

浓度= <所有读数的平均值>％+/- 2 x s％

例如：若在正确率为95％的情况下确定我们的浓度为20％+/- 0.2，则s必须等于0.1。

然而，对于光谱学，这还不够准确，我们还需要考虑额外的变量。我们将在下一篇博客中介绍这些内容。