1.引言

       在研究晶体振荡器和原子钟的稳定性时，人们发现这些系统的相位噪声中不仅有白噪声，而且有闪烁噪声。使用传统的统计工具（例如标准差）分析这类噪声时统计结果是无法收敛的。为了解决这个问题，David Allan于1966年提出了Allan方差分析，该方法不仅可以准确识别噪声类型，还能准确确定噪声的特性参数，其优点在于对各类噪声的幂律谱项都是收敛的。该方法初被用于分析晶振或原子钟的相位和频率不稳定性，比如，晶振的中心频率均采用Allan方差来表征时域内的稳定度。由于gao端陀螺，气体传感等各类物理量测仪器本身也具有晶振的特征，因此该方法随后被广泛应用于各种物理传感器的随机误差辨识中。

这些是本文即将涵盖的主题。

       下文中，我们首先将从整体上介绍传感器噪声的基础知识。有了噪声知识，我们将讨论Allan方差图的含义，帮助你在购买产品中使用这些数据进行决策以及在使用产品时校正传感器的噪声。

2.信号，噪声和数据

2.1.噪声

       这只是一个纯粹的定义，但将对我们的分析很有帮助。如果这个定义不正确，则信号中不趋近于零的部分就不是“噪声”，而是其他的东西。可能是某种干扰，可能是传感器的偏移量，甚至，可能就是你要测量的数据！信号中不是噪声又不是实际数据的部分通常称为“错误”。在现实世界中的数据流（即信号）中，所有这些因素和其他因素共同构成了传感器输出的值。以加速度计为示例：

       即使这样，我们也无法使用单个数据点来很好地校正噪声。首先，噪声水平通常是“大”噪声。这意味着噪声将偏离实际数据值约0.01g，但其幅度也可能更小。即使我们假设噪声始终为0.01g，该特定数据点上的噪声是叠加还是降低？换句话说，我们的测量值实际上是1.062还是1.042？没有办法知道。

测量噪声

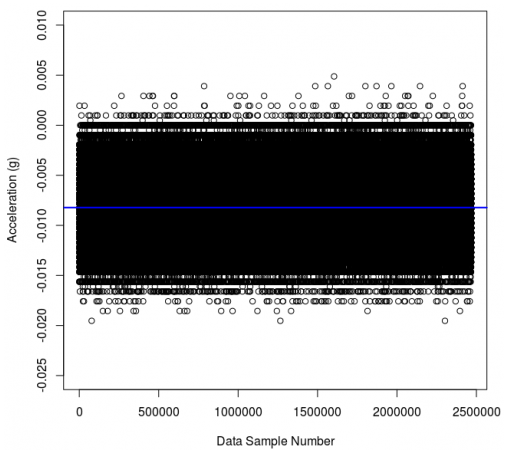
       如果将所有这些值取平均值，我们将得到沿蓝线的值。它非常接近零，为-0.008。这里可能涉及到准确性的问题（我们将在今后的文章中介绍有关准确性Accuracy和分辨率Resolution的定义和应用）。但是由于该传感器已经过校准，因此上述偏差的原因更可能是由于加速度计相对于地球重力矢量略有倾斜引起的，这会导致加速度在X或Y方向上存在一定的分量。

       但是，你可能会想：这种分析仅在我们不想测量任何变化的数据时才会有效。因为你买加速度计可不只是为了测重力，你实际上希望它能够移动——在真实应用环境中测量加速度随时间的变化。为此，我们需要表征噪声随时间变化的情况，因此需要找出能够校正噪声之前，要采集数据的时间长度。

3.Allan方差

       对于许多传感器而言，存在一段理想的时间长度，在该时间长度上取平均值（或其他统计参数）可以获得噪声的小值（至少对于某些类型的噪声）。以上面的250万个点为例，我们可以问一个问题：要以较高的信噪比达到-0.008的期望值，我们需要至少平均多少个点？这是一个很好的问题，但不幸的是，对于所获取的数据集，直到获得很多数据点之后，我们才知道-0.008这个“答案”。

       现在，我们将每个单独的数据点视为一个“组”，而不是由125万个点组成的两组。也就是说，我们现在有250万个“组”。在这种情况下，我们做同样的事情——“平均”每个组（在这种情况下，每“组”只有一个数据），然后检查所有组平均值之间的方差。当将每个单独的点视为一个“组”时，组平均值的方差就等于传感器在以每个点的平均时间为间隔时的噪声。以上述传感器为例，两侧的平均值大约为0.01g（总计0.02g）。

       为此，我们不仅要有一个或125万个小组，而且要尝试所有组的规模。因此，我们可以遍历整个数据集，并将其分成由2个数据点构成的组，然后分别平均。然后以3，4，5 .... 10 .... 100 .... 1000等个数据点为组，分别进行平均。后我们找到所有大小相等的数据组之间的方差。随着数据组变得越来越长，不同数据组之间的平均值会越来越接近，因为每个数据组的平均值会越来越接近“真实”的平均值。

       幸运的是，网上已经有很多程序可以让我们做Allan方差计算。其文档和资源可在线获得。我们利用这些程序可得到如下图：

       该图显示了我们期望的结果（即，确实存在一个非常明显的点，对足够大的一组数据求平均会使噪声水平比数据数量较少的组小）。但是，这个图并不是非常有用，有两个原因：

• 这种变化过于剧烈，以至于很难说出理想的组数是多少 

• 方差的单位是传感器值的平方，而“加速度平方”不是一个很直观的单位 

还有一个奇怪的事实是，方差在下降之后会再次上升，我们稍后再来讨论这点。

       不过，我们可以通过将数据放在对数——对数图上来解决di一个问题。下降之所以如此急剧，是因为方差在较短的横轴区间内下降了几个数量级。因此，对数——对数图将给较小的数字更大的权重，并加重变化。我们可以使用Origin或者Matlab将上述数据重新作图，将横轴和纵轴都更改成对数坐标，从而得到如下图：

       在di一个线性图中方差的平方增加对应对数——对数图中的显著转折。即使在线性图上，也可以清楚看到与初始的噪声降低相比，噪声也只是略有上升的趋势。