(1)拉力机,冲击试验机的功能原理
根据理论力学的原理，我们知道势力场中，有势力的功等于质点（系）始末两位置势能之差。由功能原理，有势力的功等于质点（系）始末两位置动能之差。因此，无论是落锤冲击试验机还是摆锤冲击试验机，下式恒成立：
m一冲击锤质量；
g一试验机工作当地重力加速度
LA一冲击锤在4点位置高度；
LB一冲击锤在S点位置高度；
VA一冲击锤在4点位置速度；
VR一冲击锤在B点位置速度。
式（2-43)中，系统内的势能和动能（地球的动能看着不变）是可以相互转换的：势能的增加等于动能的减少，而动能的增加等于势能的减少。上式也可写成：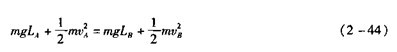


式（2-44)左边表示冲击锤质心在位置/I时的系统的机械能，公式右边表示冲击锤质心在位置A时的系统的机械能。公式右边表明，在系统内的势能和动能相互转换过程中，系统的总机械能保持不变。因此有机械能守恒定律：
如果一个系统内只有保守力（如果重力、弹性力）作功，其他内力和一切外力都不做功 (或其他内力和一切外力的总功为零），那么，系统内各物体的动能和势能（重力势能、弹性势 能）可以互相转换，但是，他们的总和保持不变。

(2)落锤冲击试验
落锤冲击试验机试验时，将质量为m重锤提升到位置A (距试样接触表面距离为H)高度后，对试样进行冲击试验，由机械能守恒定律得公式（2-44)，可以分别计算下列结果。
a)落锤的冲击速度
已知落锤冲击点距试样接触表面髙度为H，落锤的动能为零，并且取此为坐标零点，方向向下为正。又当落锤自由下落至试样接触表面时，落锤冲击点至zui低位置，落锤的势能为零，因 此，由式（2-44)，


在整个冲击过程中，作用在冲击锤上的力有两个，一个是锤的重力f，另一个是试样对锤的正压力。由于重锤在整个过程中，它的初、末速度均为零，也即它的初、末动量均为零，如果取竖直向上的方向为坐标轴的正方向，那么，根据动能原理，得：


由式（2-46)可以看出，重锤自由下落时产生的冲击力与锤的重力、下落高度成正比关 系、与试样的作用时间成反比关系。
为方便看出正压力P与冲击高度及作用时间r的关系，假设重锤的冲击高度H=14.7m,锤 重F= 1N时。按照上式计算得相应结果如表2-2。
表2-2落体冲击力与离度，作用时间的关系
 

在其他条件不变的条件下，正压力作用时间越短，重锤产生的冲击力越大，当作用时间为 0.1s时，重锤产生的冲击力竟达到其静重的20倍。

(4)摆锤冲击原理
我们可以将摆锤式冲击试验机的摆当作绕定轴转动的刚体。在重力场，当摆锤处于初始扬角a处时，具有一定的势能，动能为零；自由下落至zui低点，势能转换为动能， 这时势能为零，转换为zui大动能。试验时，具有巨大动能的摆锤冲击试样，试样在破坏过程中吸 收部分摆锤动能，摆锤在剩余动能的驱使下继续前冲直至动能为零的一个新位置后回落，这个摆 锤在冲断试样后继续前冲直至动能为零的一个新位置就可表示为试样破坏所消耗的能量。
 
上式确定了碰撞冲量作用点K的位置。只有作用于刚体的碰撞冲量的作用线在刚体对称平 面内，并垂直于质心的转动半径，作用线到转轴的距离= 才能使（具有与转轴垂直的 对称面）的转动刚体在转轴处不产生碰撞冲量。这个K点称为打击中心，A称作打击中心距。
由于在检测过程中，并不容易求得摆锤式冲击试验机作为转动刚体的质心和转动惯量乃， 因为，通常只有技术人员在设计摆锤时用于计算打击中心位置。所以，我们可以根据刚体绕定轴 转动的微分方程来导出计算打击中心距的简捷公式。

因此，可以测量摆的微幅摆动周期来确定摆的转动惯量。有利于操作拉力机与冲击试验机的工作人员以及,仪器计量、仪器校准、检测人员在现场使用,作为一个参考.

上面我讲述了拉力机与冲击试验机的结构原理,我们来看一款恒宇的拉力机

安全鞋冲击试验机

拉力机,微电脑式拉力试验机