1.脉动流特性
几乎所有的管道流都是不稳定的,不论是层流状态还是湍流状态下都存在各种干扰。所谓脉动流是指流体在测量区域的流速是时间的函数,但在一个足够长的时间段内有一个恒定的平均值,这个值决定于脉动流的流动规律。
真正的管道定常流仅出现在层流中,大多数工业管流均出现湍流现象,试试一种统计意义上的定常流,脉动流会影响涡轮流量计的测量度,有时会使其测量值严重失真,所以工业上迫切需要研究脉动流对其测量度的影响。
我们通常只能测量出脉动的主要参数,如辐值、频率和波形,然后通过这些参数分析脉动可能给流量计造成的影响。
2.脉动流对涡轮流量计测量精度的影响
特性方程及计算
涡轮流量计以动量矩守恒定理为基础的一种速度式流量仪表,对非稳定流由于转子叶片和相关传动装置的共振、转子的转动惯量、脉动的形状、转子和齿轮摩擦阻力及转子瞬时转矩等因素影响,使涡轮流量计产生很大的误差,用机翼理论来分析作用在转子上的驱动力矩和阻力矩,可得到其运动方程:
式中J为叶片转动惯量,θ为叶与轴线之间的夹角,r为涡轮叶片的平均半径,A为管道流量面积,ρ为流体密度,ω为涡轮的旋转角加速度,Q为通过管道流量。
若把脉动流表示为Q=asin2πfpt,经过分析整理,可得出涡轮旋转角加速度与脉动流各参数的关系:22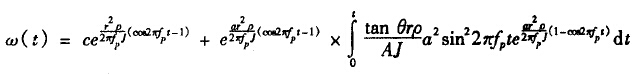
其中C为稳态时的ω值。
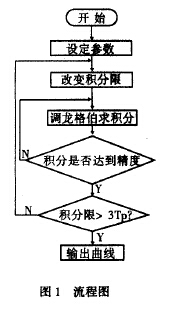
对特定的涡轮流量计和不同的脉动流,可编程计算出(2)式在脉动周围内各离散点所对应的ω(t),据此计算可画出ω(t)曲线,其流程图如图1:
2.2结构与分析
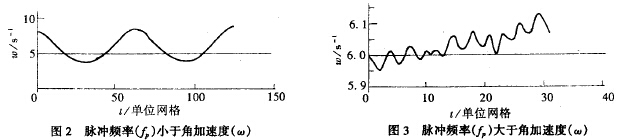
经过计算分析,发现导致流量计产生误差的主要因素是脉动流的频率,所加的正弦脉动流的频率与稳态下涡轮的旋转角加速度的关系为ω=2πfp(1/qm)r2时,相应曲线与输入正弦曲线zui为接近,与理论分析基本吻合,多次改变脉动流频率、振幅参数,发现有时图形失真非常厉害,通过对多幅图形的比较,发现有如下规律:(见图2、3)
|  |
3.结论
从以上分析计算可知,脉动流频率对涡轮流量计的测量精度影响zui大,当脉动频率fp小于旋转角加速度ω时,流量仪表的响应曲线与输入脉动曲线相似,测量结构接近于真值;脉动振幅对涡轮流量计的测量精度存在影响,但当脉动振幅小于某一振幅值时,可认为其不影响涡轮流量计的精度;叶片转动惯量J和叶片的初始旋转加速度C也对涡轮流量计测量精度有影响。
本文由江苏德图仪表有限公司为您提供,转载请注明出处!!




